Euler, Erdős

I recently gave an introductory talk that was focused on the aptly-named Outer space; you can follow the first link if you'd like to see the abstract and slides. Besides telling people about this cool space, the talk was also meant to highlight some beautiful ideas that are useful toolkits in geometric group theory (GGT). It is in this spirit that I ended up including a comment in the talk about playing ping-pong to get a presentation of the group \(GL(2, \mathbb Z)\). In all honesty, it was not something I'd ever done myself. In fact, I'd only ever seen the details of playing ping-pong once before; my professor worked it out explicitly in my first GGT class (Fall 2015) and I did not understood it at all back then. I was happy to just accept on faith as a thing that can be done whenever I saw it mentioned in the wild. A bit more concerning, the context in which I'd made the comment was more general than the typical ping-pong use case. This post is me working out the details of that comment, convincing myself I didn't lie to my audience!

First things first,

Why do group theorists play ping-pong?

The “ping-pong lemma” is nice way for ensuring you have a free subgroup at hand — whatever that means. I think it's an idea best illustrated by examples. I'll even start with a non-example just to be safe.

Consider the set of positive real number \(\mathbb R_+\). Multiplication makes this set a group: with any two positive numbers \(x = 1.1\) and \(y = 2.3\), you can multiply them to get a new number \(xy = 2.53\); and with any positive number \(z = 4.5\), there is an inverse \(Z = \frac{1}{4.5}\) that multiplies with \(z\) to cancel: \(zZ = 1\). The numbers generated by \(2\) and \(3\), which I'll call \(N(2,3)\) for short, are those you can get by multiplying a bunch of \(2,~\frac{1}{2},~3,\) and \(\frac{1}{3}\) together (in some order). For example \(\frac{2}{3}\) is in \(N(2,3)\) because you can get it by multiplying \(2 \cdot \frac{1}{3}\).

To appreciate what a free subgroup is, let's first see what it isn't, i.e. why \(N(2,3)\) is not a free subgroup. It isn't free because you can get \(1\) by multiplying \(2 \cdot 3 \cdot \frac{1}{2} \cdot \frac{1}{3}\): at each multiplication point, you have \(2 \cdot 3\), \(3 \cdot \frac{1}{2}\), and \(\frac{1}{2} \cdot \frac{1}{3}\), none of which cancel; yet altogether, everything cancels!

A free subgroup is more-or-less when nothing like this is possible — if nothing cancels at each multiplication point, then everything doesn't cancel in the end. The non-example is a subgroup that isn't free.¹ So a group theorist will “play ping-pong” to confirm a subgroup is free, or more generally, to confirm a subgroup is as free as possible.

With the “why” out of the way,

How do group theorists play ping-pong?

To get interesting free subgroups, we will have to leave \(\mathbb R_+\) behind and look to another group, \(SL(2, \mathbb Z)\): this is the set of 2-by-2 integer matrices with determinant \(\,1\); matrix multiplication makes it a group. For specific elements in the group, I will use:

\[a = \begin{pmatrix}1 & 2 \\ 0 & 1\end{pmatrix} \quad \text{and} \quad b = \begin{pmatrix}1 & 0 \\ 2 & 1\end{pmatrix}.\]

I will use capital letters A and B to talk about the inverses of a and b. The matrices generated by a and b, which I'll call M(a,b) for short, are those you can get by multiplying a bunch of a, A, b, and B together in some order. For example \(\begin{pmatrix}-3 & 2 \\ -2 & 1 \end{pmatrix}\) is in M(a,b) because you can get it by multiplying aB. Let's see how playing ping-pong confirms that M(a,b) is a free subgroup.

To this end, I am going to give a description of how the matrices a, A, b, and B transform the \(xy\)-plane. Points in the plane can be written as column vectors and I want you to focus on these four:

\[ p_1 = \begin{pmatrix}1 \\ 0\end{pmatrix}, \quad p_2 = \begin{pmatrix}1 \\ 1\end{pmatrix}, \quad p_3 = \begin{pmatrix}0 \\ 1\end{pmatrix}, \quad \text{and} \quad p_4 = \begin{pmatrix}-1 \\ 1\end{pmatrix} \]

Here's a picture of the \(xy\)-plane, with the diagonal lines and the four points included:

Fig. 1. The \(xy\)-plane.

Let's see what happens when you multiply some of these points with a:

\[ a \cdot p_1 = \begin{pmatrix}1 & 2 \\ 0 & 1\end{pmatrix} \begin{pmatrix}1 \\ 0\end{pmatrix} = \begin{pmatrix}1 \\ 0\end{pmatrix} = p_1 \qquad \text{and} \qquad a \cdot p_4 = \begin{pmatrix}1 & 2 \\ 0 & 1\end{pmatrix} \begin{pmatrix}-1 \\ 0\end{pmatrix} = \begin{pmatrix}1 \\ 1\end{pmatrix} = p_2 \]

So a fixes \(p_1\), sends \(p_4\) to \(p_2\), and (you should check this) \(p_2\) to somewhere to the right between the diagonal and the \(x\)-axis. You can do the same with with b; the next picture is an illustration of the two transformations:

Fig. 2. The left and right figures are the before and after pictures of the \(xy\)-plane.

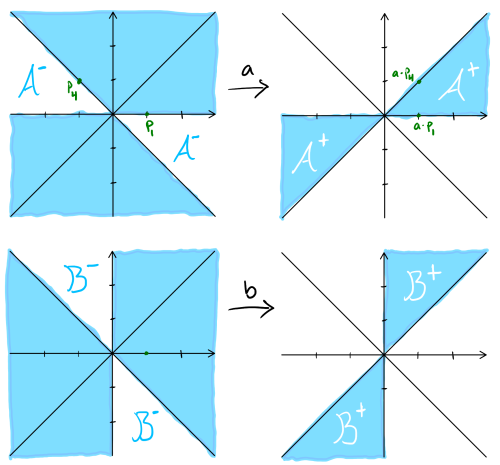
Notice how the shaded regions \(\mathcal A^+\) and \(\mathcal B^+\) in the two after pictures don't overlap? Do you also notice how the blank regions \(\mathcal A^-\) and \(\mathcal B^-\) in the before pictures don't overlap either?! In fact, altogether the regions \(A+\), \(\mathcal A^-\), \(\mathcal B^+\), and \(\mathcal B^-\) don't overlap! This means the subgroup M(a,b) is free!!² This is the ping-pong lemma in a nutshell!!!

In practice, the thing you have to do is find compatible “shadings” for your two elements x and y; by compatible, I mean the “after-shaded” and “before-blank” regions do not overlap. Once you have that, the ping-pong lemma says the subgroup generated by x and y is free.

Now that I've told you what the ping-pong lemma says, you're probably wondering:

Where does the term “ping-pong” come into play?

The playing is in the proof (and the proof is in the pudding, ha!)! Let's prove (by example) that M(a,b) is free. Remember from the \(N(2,3)\) non-example before, the expression \(2 \cdot 3 \cdot \frac{1}{2} \cdot \frac{1}{3}\) cancelled out even though no cancelling happens at any multiplication point. The point of the proof is that the same expression abAB in M(a,b) will not cancel out. In fact, there is a point in the \(xy\)-plane which is not fixed by abAB.

For the expression abAB, choose a point \(q_0\) that is not in \(\mathcal A^+\) (because a is the first letter) and not in \(\mathcal B^+\) (because B is the last letter). I'll now explain why \(abAB \cdot q_0 \neq q_0\) with a four-shot rally of ping-pong between player a/A and player b/B. I'm also including a picture of the rally to help you follow the game.

Fig. 3 [Not Drawn To Scale]. The epic ping-pong rally narrated below.

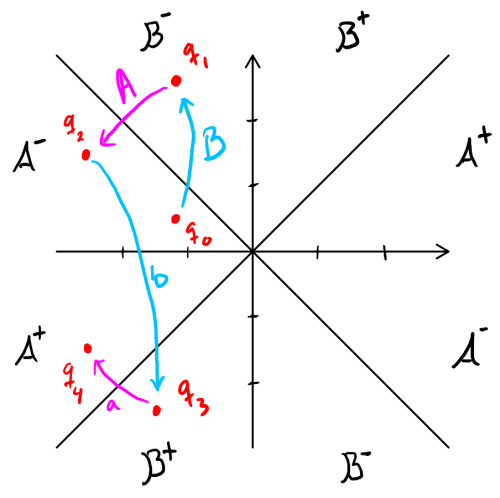
1. Since \(q_0\) is not in \(\mathcal B^+\), i.e. \(q_0\) is in the blank region of the after-b-picture, then \(q_1 = B \cdot q_0\) is in the blank region of the before-b-picture, i.e. \(q_1\) is in \(\mathcal B^-\). This first step is the serve in our game of ping-pong where b/B hits the ball from its position \(q_0\) to its next position \(q_1\) in \(\mathcal B^-\).
2. But \(\mathcal B^\pm\) and \(\mathcal A^\pm\) don't overlap, so \(q_1\) is not in \(\mathcal A^+\), i.e. \(q_1\) is in the blank region of the after-a-picture, and \(q_2 = A \cdot q_1\) is in the blank region of the before-a-picture, i.e. \(q_2\) is in \(\mathcal A^-\). This second step is the return of the serve in our game where a/A hits the ball from \(q_1\) to \(q_2\) in \(\mathcal A^-\).
3. Once again \(\mathcal B^\pm\) and \(\mathcal A^\pm\) don't overlap, which puts \(q_2\) in the shaded region of the before-b-picture and \(q_3 = b \cdot q_2\) in \(\mathcal B^+\). This is the third shot by b/B from \(q_2\) to \(q_3 \in \mathcal B^+\).
4. No overlapping means \(q_3\) is in the shaded region of the before-a-picture and \(q_4 = a \cdot q_3 \in \mathcal A^+\). This is the winner by a/A from \(q_3\) to \(q_4\).
5. All in all, the game started with the ball at \(q_0 \notin \mathcal A^+\) and ends with the ball at \(abAB \cdot q_0 = q_4 \in \mathcal A^+\). Therefore, \(abAB \cdot q_0 \neq q_0\)!

The same argument works for expressions like aabbABaabaBAABBB where consecutive a/As or b/Bs should be read in blocks representing really hard hits in the rally. The only thing I needed to make the argument work was the assumption that there is no aA, Aa, bB, nor Bb appearing in the expression; this is exactly the assumption that no cancellation happens at any multiplication point.

Are there other ways to play ping-pong?

I'm glad you asked! That's actually why I'm writing this post. The comment that I made in my talk was not about free subgroups but instead freely amalgamated subgroups. This time I'll use:

\[c = \begin{pmatrix}0 & -1 \\ 1 & 0\end{pmatrix}, \quad \quad d = \begin{pmatrix}0 & -1 \\ 1 & 1\end{pmatrix}, \quad \text{and} \quad e = \begin{pmatrix}-1 & 0 \\ 0 & -1\end{pmatrix}.\]

These matrices have finite order: the expressions \(c^4\), \(d^6\), and \(e^2\) all cancel out; already, this means the subgroup \(M(c)\) (, \(M(d)\), and \(M(e)\) resp.) generated by \(c\) (, \(d\), and \(e\) resp.) is not free. Another interesting relation happens: \(c^2 = d^3 = e\); this relation says \(M(e)\) is in the intersection of \(M(c)\) and \(M(d)\). Because of all these relations, the subgroup \(M(c,d)\) generated by \(c\) and \(d\) cannot be free. However, a variation of the ping-pong game can tell us that there are no other relations in \(M(c,d)\)! That is, the subgroup is as close to being free as is possible, given these constraints. For short, I'll write:

\[M(c,d) \cong M(c) *_{M(e)} M(d).\]

In the new version of ping-pong, I need to find a single shading of the \(xy\)-plane that satisfies three conditions:

1. \(c\) maps the shaded region into the blank region;
2. \(d\) and \(d^2\) map the blank region into the shaded region; and
3. \(e\) maps shaded to shaded, blank to blank.

You don't need to worry about what \(c\) does to the blank region nor what \(d\) and \(d^2\) do to the shaded region.

Here's a shading that gets the job done:

Fig. 4. Shading: “I get the job done.”

I'll now briefly prove this variation of the ping-pong lemma. This is yet another proof by example if that's alright with you: the expression \(cdcd\) is reduced since it is an alternating product of \(c\)'s and blocks in \(\{d, d^2 \}\); I need to convince you that it doesn't cancel out. If it did cancel out, then so would \(d^2cdcd^5\) because \(d^6\) cancels out; and for the same reason, if \(d^2cdcd^5\) did cancel out, then so would the original expression \(cdcd\). And as \(d^3 = e\), I can rewrite (reduce) the new expression: \(d^2cdcd^5 = d^2cdcd^2e\). I prefer this last reduced expression because, ignoring the \(e\) at the end, it start and ends with blocks in \(\{d, d^2 \}\). Here's a five-shot rally of ping-pong between players c and d/dd:

1. referee e toss the ball up from a blank position to a blank region;
2. dd volleys from the blank region to a shaded region;
3. c returns the volley from a shaded region to a blank region;
4. d hits from blank to shaded region;
5. c hits from shaded to blank region; and finally,
6. dd hits a winner from blank to shaded region.

Fig. 5. Another ping-pong rally for the ages.

The game started at a blank position and ended at a shaded position; therefore, \(d^2cdcd^2e = d^2cdcd^5\) doesn't cancel out! This in turn means the original expression \(cdcd\) doesn't cancel out either.

The presentation of \(GL(2,\mathbb Z)\), as promised.

Using the Euclidean algorithm (e.g. row-reduction), you can verify the elementary matrices \(cd^5 = \begin{pmatrix}1 & 0 \\ 1 & 1\end{pmatrix}\) and \(c^3d = \begin{pmatrix}1 & 1 \\ 0 & 1\end{pmatrix}\) generate \(SL(2,\mathbb Z)\). Therefore, \(SL(2,\mathbb Z) = M(c,d)\) and, by the ping-pong game above, \(SL(2,\mathbb Z) \cong M(c) *_{M(e)} M(d).\)

You can check that the transposition \(\tau = \begin{pmatrix}0 & 1 \\ 1 & 0\end{pmatrix}\) conjugates \(c\) to \(c^3\) and \(d\) to \(d^5\) (also \(e\) to itself), i.e. \(\tau c \tau = c^3\) and \(\tau d \tau = d^5\) (\(\tau e \tau = e\)). Yet \(\tau\) and \(SL(2,\mathbb Z)\) generate \(GL(2,\mathbb Z)\): the set of 2-by-2 integer matrices with determinant \(\,\pm 1\). And just like \(e\) did, \(\tau\) preserves the shading for the ping-pong game. This leads to semi-direct product descriptions:

\[\begin{aligned} GL(2,\mathbb Z) = M(c,d, \tau) &\cong \left( M(c) *_{M(e)} M(d) \right) \rtimes M(\tau) \\ &\cong \left( M(c) \rtimes M(\tau) \right) *_{M(e) \times M(\tau)} \left( M(d) \rtimes M(\tau) \right). \end{aligned}\]

But \(M(c)\), \(M(d)\), and \(M(e)\) are cyclic subgroups of order \(4\), \(6\), \(2\) respectively; so the corresponding products in the last line are dihedral groups \(D_4\), \(D_6\), and \(D_2\) (of order \(8\), \(12\), and \(4\) resp.). Finally,

\[GL(2,\mathbb Z) \cong D_4 *_{D_2} D_6.\]

And because I can't help myself, I have to leave you with a question: does the free subgroup \(M(a,b)\) have finite index in \(GL(2,\mathbb Z)\)?