Euler, Erdős

It's been a while since my last post but I feel like my first published paper is a worthy reason to break the blogging hiatus. When I first started the blog as an undergraduate, I meant it to be a record of my investigations outside the curriculum. Graduate school took up all my time and focus for these forays. I also thought it would be impossible to write about my graduate work in an accessible way. But with school done now, I have no reason not to try! So here I am giving it a looong shot.

The paper's titled "Irreducible nonsurjective endomorphisms of \(F_n\) are hyperbolic"; I've got 2 goals for this post:

1. I'd like to explain what most of the terms in the title mean and give somewhat of a reason why the results in the paper are interesting to me.
2. I want to mention some behind-the-scene moments of the paper. One common problem with the way we write math papers is that it hides how these theorems and proofs come about in the first place. If I am able to demistify any aspect of that process, I will consider it a success no matter how small.

Free Groups

^{Next Section}

Alright, let's now dive into the paper's title. What is \(F_n\)? This stands for "free group of rank \(n\)" where \(n\) is some positive integer. For this post, I'll start with \(n = 2\) and later \(n = 3\). So what is the free group of rank 2? Choose your favorite two (\(n = 2\)) letters, say \(a\) and \(b\), then \(F_2\) is the set of words (not necessarily real words) you can write out of these two letters; e.g., abab, abA, and BBBAAA are words in \(F_2\). You are allowed to mix uppercase (capital) and lowercase (small) letters with the exception that a and A cannot follow each other and same goes for b and B. That means \(F_2\) does not contain words like aA or aBb. All in all, whenever I write \(F_2\), you can simply think of words using those two letters.

In fact, the things I'll be focusing on aren't the words in \(F_2\) but the strings in the free group. Strings in \(F_2\) are biinfinite words using the two letters; e.g., ⋯abababab⋯, ⋯abABabAB⋯, and ⋯abbabaab⋯ are strings in \(F_2\). The strings can be (but don't have to be) repeating; the restriction is the same as the one on words: a/A and b/B cannot follow each other. Two strings will be considered "the same" (equivalent) if they only differ by some shift to left/right; e.g., the repeating-strings ⋯ababab⋯ and ⋯bababa⋯ are the same since they both encode the pattern of alternating a's and b's. I could (but won't) also insist strings be the same if they are inverses of each other as these essentially encode the same pattern but from opposite direction.

Endomorphisms of Free Groups

^{Previous Section, Next Section}

Now I can define the next big term in the title. What is an endomorphism of \(F_2\)? An endomorphism of \(F_2\) is a kind substitution rule that is best explained by example. A rule could replace a with ab and b with ba, which is usually written as: a\(\mapsto\)ab and b\(\mapsto\)ba. You can now apply this rule to other words/strings in \(F_2\); e.g., aabb\(\mapsto\)ababbaba, ⋯aa⋯\(\mapsto\)⋯abab⋯, or ⋯abba⋯\(\mapsto\)⋯abbabaab⋯. The tricky bits are the inverses (capital letter): A is not replaced with AB but BA! You not only capitalize but also reverse the word to find the rule for the capital letters. So A\(\mapsto\)BA and B\(\mapsto\)AB. Here's the justification of this rule: say a was the instruction "put on contact lenses" and b was "put on eye glasses", then ab says, "put on contacts then glasses"; if you understandably wanted to reverse course, you'd first take off the glasses B then the contacts A, i.e., the inverse of ab is BA.

So an endomorphism is a way of systematically replacing all words/strings of \(F_2\) with other words/strings of \(F_2\). To describe a particular endomorphism of \(F_2\), you only need to specify what words to replace the letters a and b with. Here's another endomorphism that will be useful to keep in mind: a\(\mapsto\)b and b\(\mapsto\)ab. What does this rule do to the word abAB? The first answer would be babBBA but we need to cancel the middle letters where b is followed by B to get a word in \(F_2\); so abAB\(\mapsto\)baBA, i.e., the endomorphism sends abAB to its own inverse baBA! What about BAba? Substitution gives BABabb with no cancellation needed. Finally, what happens to the repeating-string ⋯BAbaBAba⋯? The substitution and cancellation give the repeating-string ⋯ABabABab⋯ which is the inverse of the original repeating-string.

I have defined two endomorphisms of \(F_2\) for you so far and I will need some nicknames for them. The first endomorphism will be referred to as \(\psi\) and the second endomorphism as \(\phi\).

Dynamics of Endomorphisms

^{Previous Section, Next Section}

I can now state one of the things I would like to know about endomorphisms. A free group endomorphism determines a dynamical system on the words and strings of the free group by applying the substitution rule over and over again. I'm mainly interested in the dynamics on the strings. One basic question is whether there is a string that's fixed (not changed) by the endomophism; such strings are called fixed strings. If there are fixed strings, then are there also fixed repeating-strings? And maybe there aren't any fixed strings but there could be a pair of strings that get swapped by the endomorphism; like how \(\phi\) swaps ⋯BAbaBAba⋯ and ⋯ABabABab⋯. In this case, the pair of strings are called periodic strings with period \(2\).¹ The final question I'd like answered is whether there are periodic [repeating-]strings with any period. These questions are too general and, to get started, it helps to add some adjectives to restrict the scope and see what happens.

But why? To be fair, I wasn't initially interested in the answers to these questions in and of themselves. What I was thinking about (still do) was how seemingly unrelated geometric properties rely on the answers to these dynamical questions. Highlighting these connections is beyond the scope of this post that has already taken far too long (~3 months) to write as it is. But as is often the case in math, questions that were asked with specific connections in mind end up being interesting in their own right!

Nonsurjective Endomorphisms

^{Previous Section, Next Section}

The remaining words (irreducible, nonsurjective, and hyperbolic) are all adjectives used to describe endomorphisms. The easiest one to define is (non)surjective. The endomorphism \(\psi\) is nonsurjective (not surjective) because there are words like a or b that do not replace any word in \(F_2\). You can show that \(\psi\) replaces words in \(F_2\) with words twice as long; e.g., aBAb is four letters long and it is replaced with abABBAba which is eight letters long. So no word in \(F_2\) is replaced by \(\psi\) with a word of odd length like a.

On the other hand, \(\phi\) is surjective because every word replaces some word; in other words (no pun intended), \(\phi\) replaces the basis (building blocks) of our words, a and b, with another basis, b and ab. Which words are replaced with a or bABa? Just to be sure, you should check for yourself that \(\phi\) replaces bA\(\mapsto\)a and aaBAbA\(\mapsto\)bABa. The set of words you are left with after applying an endomorphism to all words in \(F_2\) is called the image of the endomorphism. The images of \(\psi\) and \(\phi\) will be written as \(\psi(F_2)\) and \(\phi(F_2)\) respectively. The endomorphism \(\psi\) is nonsurjective because its image does not contain all words, i.e., \(\psi(F_2)\) is a proper subset of \(F_2\). For instance, it is missing all words of odd length and also some words of even length; e.g., it does not contain the word aa. Compare this with \(\phi\) which is surjective because its image is all words, i.e, \(\phi(F_2) = F_2\)!

There is a related adjective that did not make it into the title that should be mentioned here. The endomorphisms \(\psi\) and \(\phi\) are all injective. This means that no two words get replaced with the same word. Injective endomorphisms are precisely the reversible substitution rules: given a word in the image of an injective endomorphism, you can recover the original word that was replaced with it. In rank 2, this boils down to asking whether the basis a and b get replaced with the same word. An endomorphism that is both injective and surjective is called an automorphism and it can be thought of as shuffling the words in the free group. For brevity's and simplicity's sake, I will assume all endomorphisms from here onwards are injective.

Unexpected Link

^{Previous Section, Next Section}

Automorphisms (surjective endomorphisms) of free groups have been a popular subject of study in (at least) the last 40 years with little room spared for nonsurjective endomorphisms. The consensus seemed to be that surjectivity made it easier to study dynamics since automorphisms have inverses: they have undo-endomorphisms so to speak. Consequently, it was expected that nonsurjective endomorphisms would be harder to study.² There's a lot of research that has been done to answer the dynamical questions posed earlier for automorphisms and close to nothing for nonsurjective endomorphisms. That's why I focused on the latter in my paper.

The surprising takeaway from my research was that nonsurjective endomorphism are (in some sense) easier to study than automorphisms! Look at the automorphism \(\phi\) for example: it is not obvious that the automorphism replaces the word abAB with its own inverse because the substitution rule when applied to abAB leads to the word babBBA that contains the letter b followed by B. It is only after cancellation that you see that the result is the inverse of the word you started with. This will be the case for most words and most automorphisms: applying an automorphism to a word in the free group will generally require cancellation. Whereas, the nonsurjective endomorphism \(\psi\) never gets to worry about cancellation! If you are like me when I first started, you are probably expecting to see cancellation in most endomorphisms just as in automorphisms and \(\psi\) is behaving like an exception to the rule. I was really shocked to realize/learn/show that cancellation is intrinsically linked to surjectivity! That is, \(\psi\)'s behavior is not an exception but the expectation. #Bars

Of course it was hard to show that nonsurjective endomorphisms are easier to study. This paper doesn't contain this general result but the beginnings of it. Patrick Reynolds was the first to prove the link for irreducible (not yet defined) endomorphisms in his 2011 PhD thesis, Dynamics of irreducible endomorphisms of \(F_n\). In Theorem 4.5 of my paper, I give what I find to be a conceptually simpler proof of Reynolds' link. For instance, Reynolds' thesis used tools developed in mid-2000s whereas my proof(s) would be accessible to a reader in 2000. The ideas in this new proof allowed me to generalize the theorem in my thesis, which you can find on my academic webpage.

Soapbox. Up until a couple of months ago, I'd been so proud of the fact that my work only used pre-2000 tools; I'd managed to say something new using "old" ideas! But it had never occurred to me that this could be viewed negatively; I don't think it has been, I hope it won't be, but it has happened for others.³ I'm no longer sure how I feel about it. I suppose I'm "proud, with an asterisk"?

Graphical Perspective

^{Previous Section, Next Section}

This section is where, like a Scooby Doo villain, I unmask and reveal my identity. I told you to think of free groups as sets of words and their endomorphisms as substitution rules, but this was only my best effort at introducing the topics to someone unfamiliar with them. But I am a geometric group theorist and that is absolutely not how I think of free groups and their endomorphisms, sorry!

Fig. 1. The standard rose and some loops & lines on it.

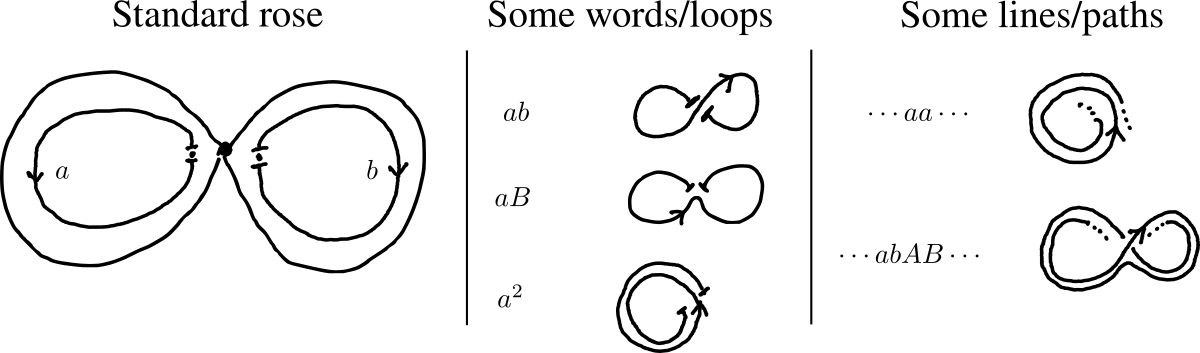
I think of them visually, in terms of graphs. A graph is a collection of vertices (think bike station) connected by edges (bike trails). The most basic graph for a free group of rank \(2\) is a rose: a graph with one vertex and two edges (See Fig. 1). Under this view of free groups, words correspond to closed paths (routes) in the rose that I'll call loops. For example, the letter a may correspond to the counter-clockwise path on the left edge and b the clockwise path on the right edge. Similarly, strings correspond to biinfinite paths called lines. Loops and lines of a graph have some restrictions too: just as a/A and b/B weren't allowed to follow each other in words/strings of a free group, don't allow a loop/line to backtrack, i.e., travel along an edge then turn and travel back the same edge. Equivalently, loops and lines shouldn't have "shortcuts"; taking shortcuts to remove backtracking is the graph-analogue of cancellation.

Thus far, the change in perspective has been mostly cosmetic. Its power lies in the fact that we could choose any other basis of the free group to correspond to the edges of the rose, e.g., b = counter-clockwise left edge and ba = clockwise right edge. A different choice of basis will be referred to as a different marking and the resultant rose with the marking is known as a marked rose. The standard rose defined in the previous paragraph is distinguished by the fact that its edges correspond to our preferred basis a and b. Informally, a marking is a dictionary that translates between words of the free group and loops of the graph. As strings/lines are built from words/loops, this dictionary will also translate between strings and lines.

Fig. 2. A marked barbell and theta graph.

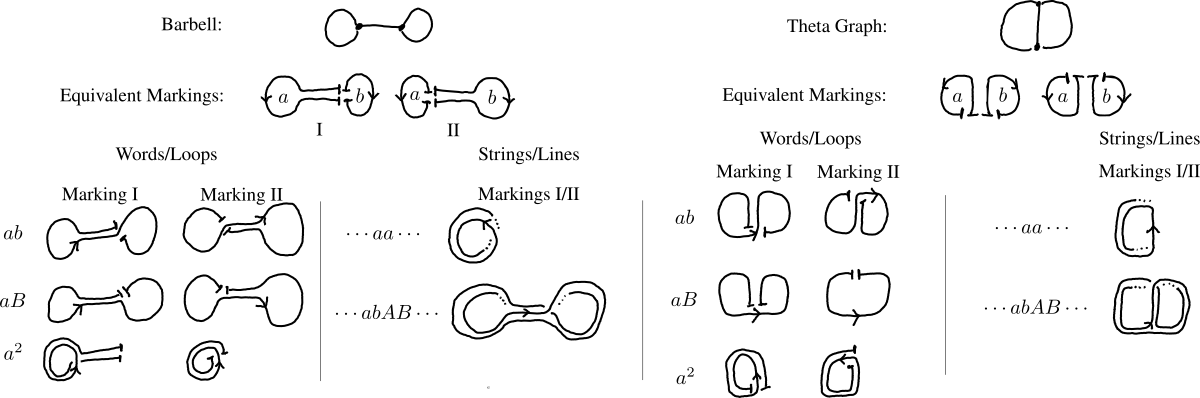
To make things more interesting, there are other graphs besides the rose that I could have used instead. In the case of rank \(2\), there are also the theta graph and the barbell (See Fig. 2). Similar to the rose, I can mark the theta graph or barbell by matching a basis with the left/right loops highlighted in the figure. Two markings are "the same" (equivalent) if their strings-to-lines translations are the same, even though words-to-loops translations might not match.⁴ Fig. 2 has examples of markings that initially look different but are the same. Informally, a marking is now a dictionary that translates between words strings of the free group and loops lines of the graph.

There's a natural topology on the set of all marked graphs to define the spine of outer space. Culler and Vogtmann introduced outer space and its spine in their 1986 paper "Moduli of graphs and automorphisms of free groups" and the spaces have been invaluable to the study of automorphisms and now endomorphisms.

Why bother with introducing the different graphs and their various markings? As I mentioned before, we don't gain much from changing perspective to thinking of words/strings as loops/paths in the standard rose. However, once we allow for other marked graphs and we choose an endomorphism of the free group, suddenly there are preferred marked graphs. These preferred marked graphs are better for studying the dynamics of free group endomorphisms!

Irreducible Endomorphisms

^{Previous Section, Next Section}

I'll switch to rank \(3\) for the rest of the post. \(F_3\) is the set of words formed out of the letters a/b/c. Let \(\varphi:F_3 \to F_3\) be the automorphism that replaces a/b/c\(\mapsto\)b/ab/ac in that order. The substitution on the first two letters a/b is exactly the same as that by \(\phi\)! To understand the dynamics of \(\varphi\), I'd have to first understand those of \(\phi\).

Fig. 3. Graph maps representing \(\varphi\).

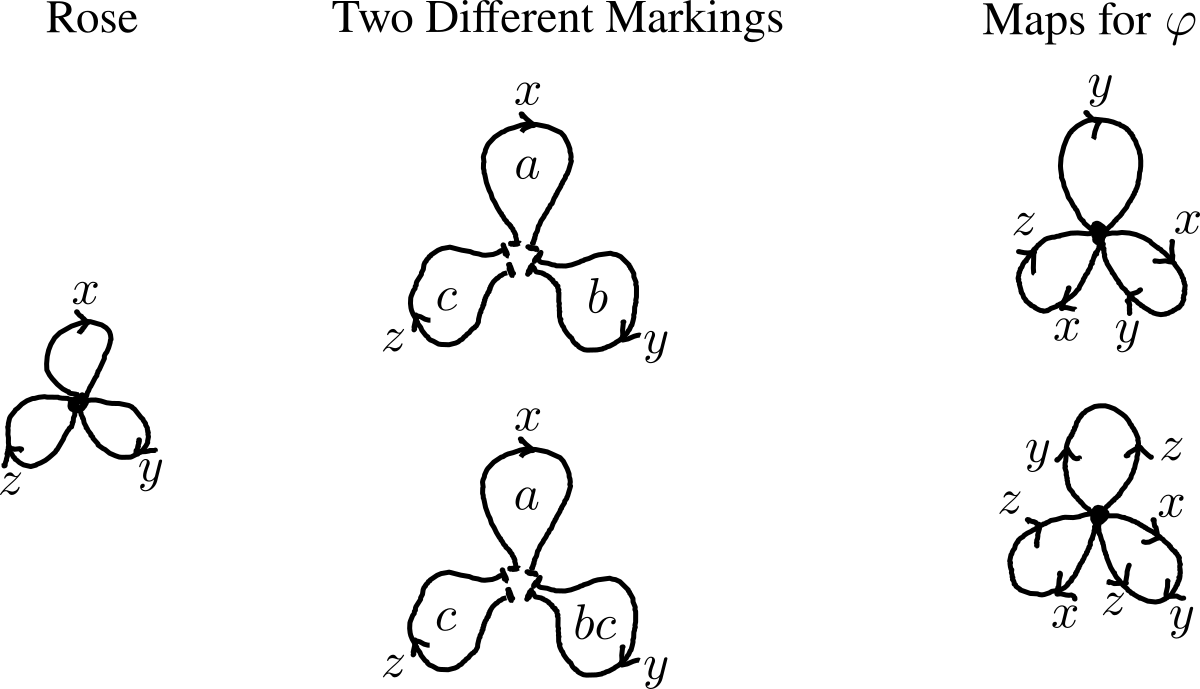
Graphically (Fig. 3), I chose two markings on the rose and used them to "translate" the endomorphism \(\varphi\) to graph maps of the rose. To avoid ambiguity, I'll orient all edges clockwise then label the top edge x, bottom-right edge y, and bottom-left edge z. The standard rose has the marking that matches basis a/b/c with edges x/y/z and the corresponding graph map sends x/y/z to the loops y/xy/xz. The top and bottom-right edges x/y form an invariant subgraph since they are sent to loops involving those same edges only. I mentioned earlier that this change is only cosmetic because it doesn't tell us anything we couldn't have read from the words. The second marked rose has the basis a/bc/c matched with the edges and its corresponding map sends x/y/z to the loops yZ/xyZ/xz. The map is represented by the graph where the edges are labelled by their images; e.g., if the y-edge is mapped to xy, then replace the y label with xy. I will only use lowercase letters and, instead, the uppercase ones like Z are indicated by switching arrow-directions. For our purposes, the second marked rose is worse since it has no invariant subgraphs and so it obscures the existence of the "smaller" endomorphism \(\phi\) hiding in \(\varphi\).

If you are given an endomorphism, sometimes you can choose a marked graph \(\Gamma\) so that the corresponding graph map \(f:\Gamma \to \Gamma\) has an invariant subgraph \(G \subset \Gamma\) as I did in the previous paragraph.⁵ When this is possible, the endomorphism is reducible and the marked graph \(\Gamma\) is a reduction-witness. Since \(G\) is a smaller graph, this reduces \(f\)'s dynamics to a smaller graph. Before you can study the dynamics of endomorphisms in general, you must first study the dynamics of endomorphisms that cannot be reduced, the irreducible endomorphisms. Think of an irreducible endomorphism as one that completely mixes the free group and makes it impossible to split its dynamics into smaller chunks. Intuitively, expect irreducible endomorphisms to have no periodic behavior in their dynamics because the mixing is so thorough.

What do we know about the irreducibility of endomorphisms \(\psi\), \(\phi\), and \(\varphi\)? Since \(\phi\) is an automorphism of a rank \(2\) free group, some linear algebra will verify \(\phi\) is irreducible.⁶ In Example 1.3 of the paper, I show that \(\psi\) is irreducible. Finally, \(\varphi\) is a reducible endomorphism whose reduction is witnessed by the standard rose. It is typically very hard to know if a given endomorphism is irreducible. In the paper, I provide two methods (Theorems 4.6 and 5.5) for verifying irreducibility but they have their blindspots and weaknesses. There's still no practical universal method for testing irreducibility of endomorphisms (Problem 1.2)!

Title Revisited. I've now defined all but one of the terms in the title of my paper, "Irreducible nonsurjective endomorphisms of \(F_n\) are hyperbolic". Endomorphisms are the main objects (or subjects? 😊) of study, irreducibility and nonsurjectivity are dynamical properties, while the remaining undefined term "hyperbolic" is geometric in nature. The title is saying that the two dynamical properties endow endomorphisms with a geometric property!

Ranking Markings

^{Previous Section, Next Section}

I mentioned the existence of preferred marked graphs earlier and the first examples appeared when discussing reducible endomorphisms: for a reducible endomorphism, its reduction-witnesses are preferred. For a nonsurjective example, let \(\rho:F_3 \to F_3\) be the endomorphism that replaces a/b/c\(\mapsto\)b/abcBA/acaCA respectively. Then the standard rose is not a reduction-witness, i.e., it has no invariant proper subgraph. But if you change the standard rose by replacing the vertex with a tripod (three edges sticking from a central vertex), then you will get a reduction-witness for \(\rho\) since the circles form an invariant proper subgraph (See Fig. 4a). The map is actually an immersion as it has no cancellation: you can check this by verifying that no pair of outgoing or incoming segments at a point share a label. The next section will describe how to find this marked graph.

Fig. 4a (top row) and 4b (bottom row). Two reductions of \(\rho\).

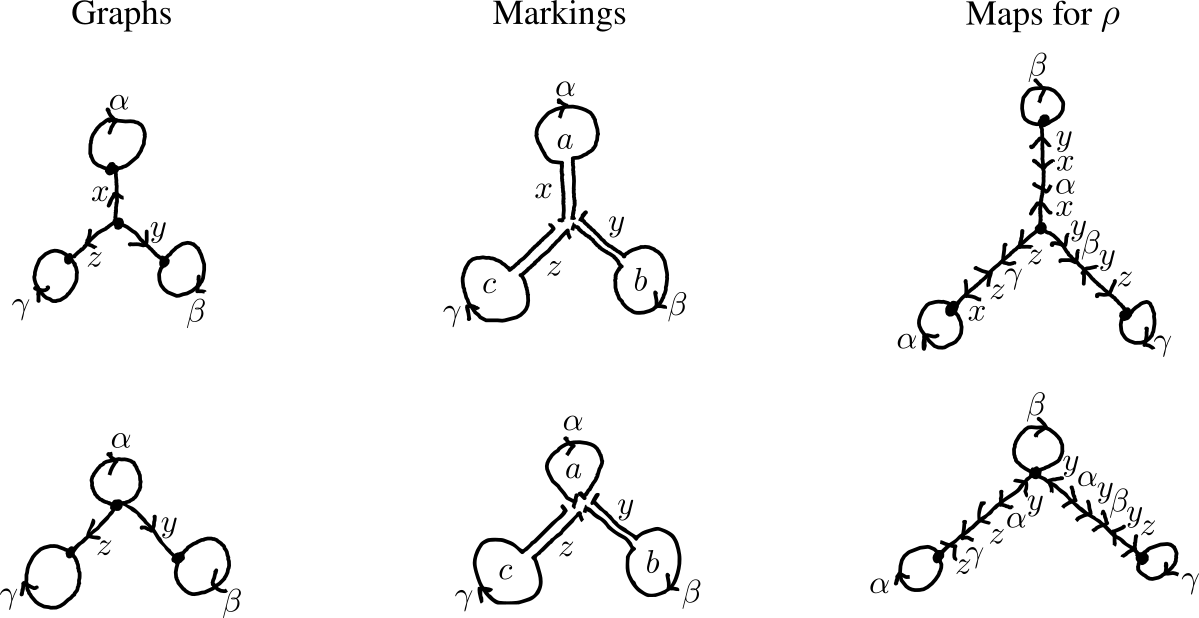
Admittedly, "preferred" is a term I'll use loosely. For instance, not all reduction-witnesses are created equal and there is another reason why the marked graph in Fig. 4a would be preferred over another reduction-witness for \(\rho\). You could have replaced the vertex with two edges sticking from a central vertex as in Fig. 4b. The corresponding map for \(\rho\) has cancellation at the center vertex as it has two incoming \(y\)-segments. The advantage of the tripod marked graph lies in the absence of cancellation. This distinction will be especially useful when considering irreducible endomorphisms which have no reduction-witnesses yet we still want to have preferred marked graphs that inform the endomorphisms' dynamics.

"What do these two marked graphs tell us about the dynamics of \(\rho\)?" you might ask. For starters, the reduction that both of them witness implies that \(\rho\) has three periodic repeating-strings (and their inverses): ⋯aaa⋯\(\mapsto\)⋯bbb⋯\(\mapsto\)⋯ccc⋯\(\mapsto\)⋯aaa⋯. However, only the immersion (top row) makes it evident that there are two other periodic strings that are inverses of each other and are swapped by \(\rho\);⁷ these last two are not repeating-strings! I have listed all the periodic strings/dynamics for \(\rho\).⁸

When studying irreducible endomorphisms, the preferred marked graphs are the ones with the least amount of cancelling, whatever that means. For automorphisms, the least amount of cancelling is a subtle thing to quantify; research in this direction was initiated in a 1992 paper by Bestvina and Handel "Train tracks and automorphisms of free groups". Generally, irreducible automorphisms have an infinite family of preferred marked graphs and these marked graphs necessarily still have some cancellation.⁹ Remarkably, Reynolds' result mentioned earlier says that irreducible nonsurjective endomorphisms have a unique preferred marked graph(!) that has no cancellation at all!! This means that irreducible nonsurjective endomorphisms have simpler dynamics than irreducible automorphisms. What Reynolds actually shows is that an irreducible endomorphism induces a map from outer space to itself with a unique fixed point — that point is our preferred marked graph and it being fixed means no cancellation. So it is a fixed point theorem, my favorite kind of theorem!

Changing Markings

^{Previous Section, Next Section}

My proof is actually similar to the proof of Banach's fixed point theorem: choose a marked graph, apply the endomorphism to it repeatedly to change the marking, then show that the change is vanishing so there is no change at the limit, i.e., the limit is a fixed point.¹⁰ That the limit is unique (Lemma 4.1) follows from Bestvina, Feighn, and Handel's work in their 1997 paper "Laminations, trees, and irreducible automorphisms of free groups".

I rely heavily on John Stallings' 1980 paper "Topology of finite graphs" that introduced folding and subgroup graphs. The new idea in the proof is a description of the change of marking using folds on subgroup graphs; this is given in Section 3 "The action of injective endomorphisms on outer space". The description is practically redundant for automorphisms but becomes crucial to seeing why nonsurjective endomorphisms have simpler dynamics.

"Fun" Fact. Patrick Reynolds and John Stallings both went to the University of Arkansas, my grad school, for their undergraduate studies: classes of 2004 and 1956 respectively.

Fig. 5. Changing of marking with folding. Top row: markings. Middle row: subgroup graphs for \(F_3\), \(\rho(F_3)\), and \(\rho^2(F_3)\).

I will now sketch a proof by nonexample. Returning back to the endomorphism \(\rho:F_3 \to F_3\) which replaces a/b/c\(\mapsto\)b/abcBA/acaCA, how did I find the marked graph in Fig. 4a? I started with the standard rose \(R_3\) and a map that represents \(\rho\). To change the marking, start with the graph representing the map (See Fig. 5, bottom-left graph). Notice how the vertex has 4 outgoing \(\alpha\)-segments? This is where cancellation happens; folding tries to get rid of the cancellation by "gluing" the segments together. Once all the folding is done, there are no more vertices that have two outgoing or incoming segments with the same label. The result is known as the subgroup graph for \(\rho(F_3)\). By keeping track of the folds and ignoring any extraneous edges/spikes, I get a marking for the subgroup graph (Fig. 5, top-center graph)

The process of folding from the standard rose to a new marked graph is what's known as a change of marking. To change the marking again, replace all segments' labels using \(\rho\) and then fold/cancel. Iterating the process gives a sequence of marked graphs that are subgroup graphs for \(\rho^2(F_3), \rho^3(F_3), \rho^4(F_3), \ldots\) The subgroup graphs will get bigger and bigger because \(\rho\) is nonsurjective! In this example, the three circles aren't growing with the rest of the graph! This means that the graphs eventually become reduction-witnesses with the "non-growing" circles forming an invariant proper subgraph. Now, if the endomorphism were irreducible, then this couldn't happen — the graphs' growth couldn't be "lopsided". However, and this is the key, the amount of cancelling happening at each iteration is limited by the folding that happened at the very first step.¹¹ Since the cancellation at each step is limited, it is actually shrinking relative to the graphs' growth. Therefore, there is no cancellation in the limit and this limit is our preferred marked graph. Q.E.F.D!

For an interesting example whose growth isn't lopsided, do the same process with the endomorphism of \(F_2\) that replaces a/b with b/bAba. Starting with the standard rose, you'll get an alternating sequence of the same marked theta graph and barbell; by collapsing their "non-growing" edges, you have a fixed marked rose! Collapsing the edges is how I pass to the limit.

Turns out I didn't even need to pass to a limit to find a fixed point for \(\rho\)! The subgroup graphs for \(\rho(F_3)\) and \(\rho^2(F_3)\) give the same marked graph because the folding wasn't enough to change the marking. This is why the corresponding map in Fig. 4a is an immersion. The fact that the process sketched above found a preferred marked graph with no cancellation for a reducible endomorphism with lopsided growth indicates that it can be generalized!

Generalization. Irreducibility was not so central to the proof. I used it to ensure that growth wasn't lopsided and also get uniqueness of the limit. But if we don't care for uniqueness, there ought to be weaker assumptions that make the rest of the argument still work like it did for \(\rho\). As a mathematician would say, irreducibility is a sufficient but not necessary condition. In the first part of my thesis, I found the necessary and sufficient condition for having a preferred marked graph with no cancellation. The condition probably allows for uniqueness too but I don't know where to even begin proving it.

Backstory

^{Previous Section}

I want to wrap up the post by giving some behind-the-scenes footage. In my first paper "Hyperbolic immersions of free groups", I proved that the geometric property of being hyperbolic is equivalent to the existence of periodic repeating-strings when an endomorphism has a preferred marked graphs with no cancellation.¹² After I'd finished writing that paper, my advisor asked me if irreducible nonsurjective endomorphisms were hyperbolic. Reynolds' result meant irreducible nonsurjective endomorphisms satisfied the hypothesis my theorem, i.e., they have preferred marked graphs with no cancellation; therefore, hyperbolicity is equivalent to the absence of periodic repeating-strings.

How and why a new proof. As I was reading Reynolds' proof, I noticed a gap that I was later able to fill with the help of Ilya Kapovich. It was in this process that I came upon the new proof that avoided the complexities Reynolds' proof dealt with. Minor as that gap was, I have it to thank for leading me on this path. It eventually got me to the most important component of my thesis a year later! I'm not sure Reynolds' methods could have been generalized the same way.

Back to periodic repeating-strings, or lack thereof. My guess had been irreducible nonsurjective endomorphisms can't have periodic repeating-string but to confirm that I had to generalize parts of of Bestvina, Feighn, and Handel's paper linked to earlier. They show that irreducible automorphisms can't have periodic repeating-strings except in well known and understood cases. However, their proof (almost) irreparably falls apart when applied to nonsurjective endomorphisms. Lemma 5.2 ended up being the missing puzzle piece that let me adapt the statements and put the proof back together. As nonsurjective endomorphisms are not part of the exceptions, they cannot have periodic repeating-strings and so they are hyperbolic. It's funny that when my advisor asked me the question mid-conversation, I answered yes right away; however, it took months before I found Lemma 5.2 and justified my answer. There's a conversation to be had here about how I could have been so convinced of my answer without a proof but it'll have to wait for another post.

How did Lemma 5.2 come about? After I was stuck for a while trying to fix/salvage the broken proof, my advisor suggested I read this paper by Borisov and Sapir. It had no direct applications to what I was working on so I think he suggested it for a change of scenery, as they say. Borisov and Sapir proved residual finiteness for endomorphisms, which is quick to show for automorphisms but quite difficult for nonsurjective endomorphisms. They end up using algebraic geometry to my surprise. I procrastinated on reading the algebraic geometry sections¹³ by looking into why exactly elementary approaches fail. One of my (all failed) attempts at reproving their theorem ended up producing Lemma 5.2, i.e., exactly what I needed in the first place!

The lemma is short and doesn't involve any sophisticated argument but, without it, there wouldn't be any paper. It completely changed how I think about endomorphisms: whenever stuck, use backward-iteration instead of forward-iteration! This idea was counterintuitive to me because nonsurjective endomorphisms don't have inverses. Nevertheless, it was essential to this paper and my thesis as well. Let me conclude on that note. Thanks for reading.

Rest in Power Chadwick Boseman

Wakanda Forever 💜